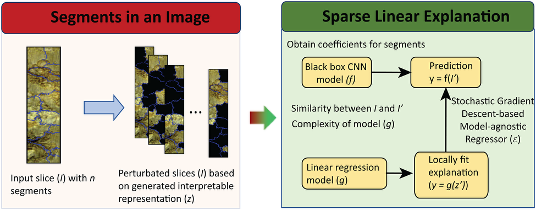
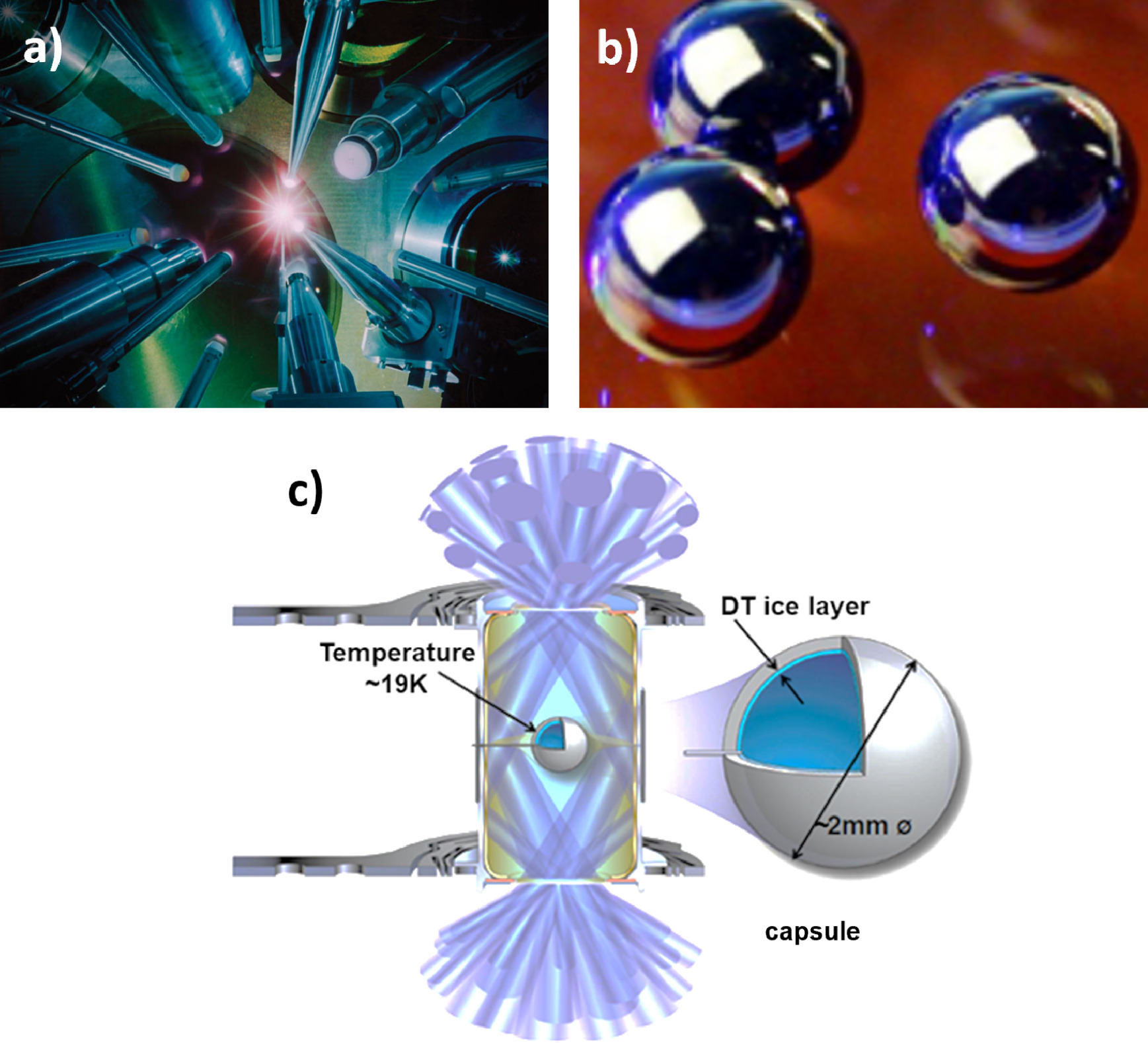
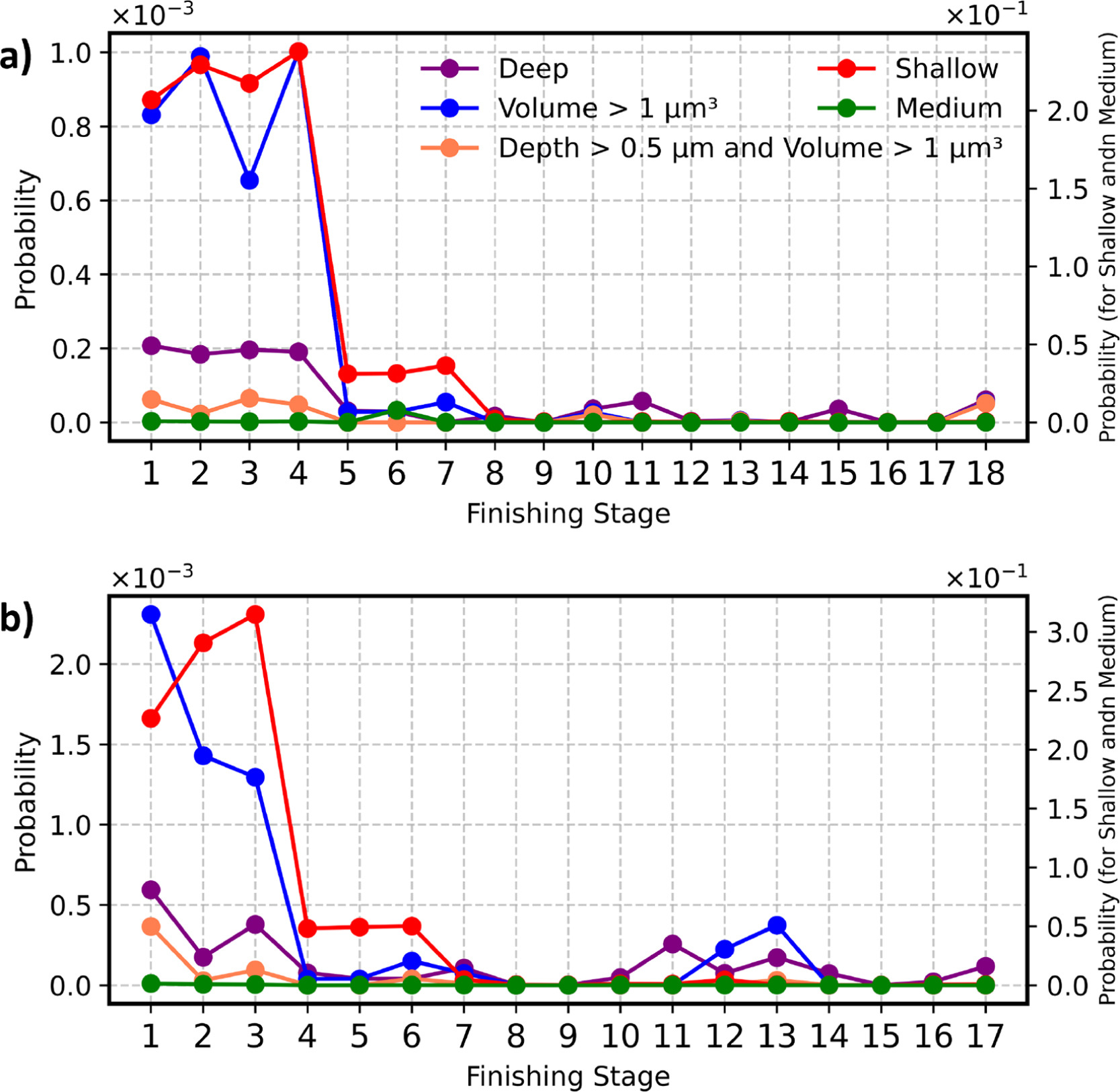
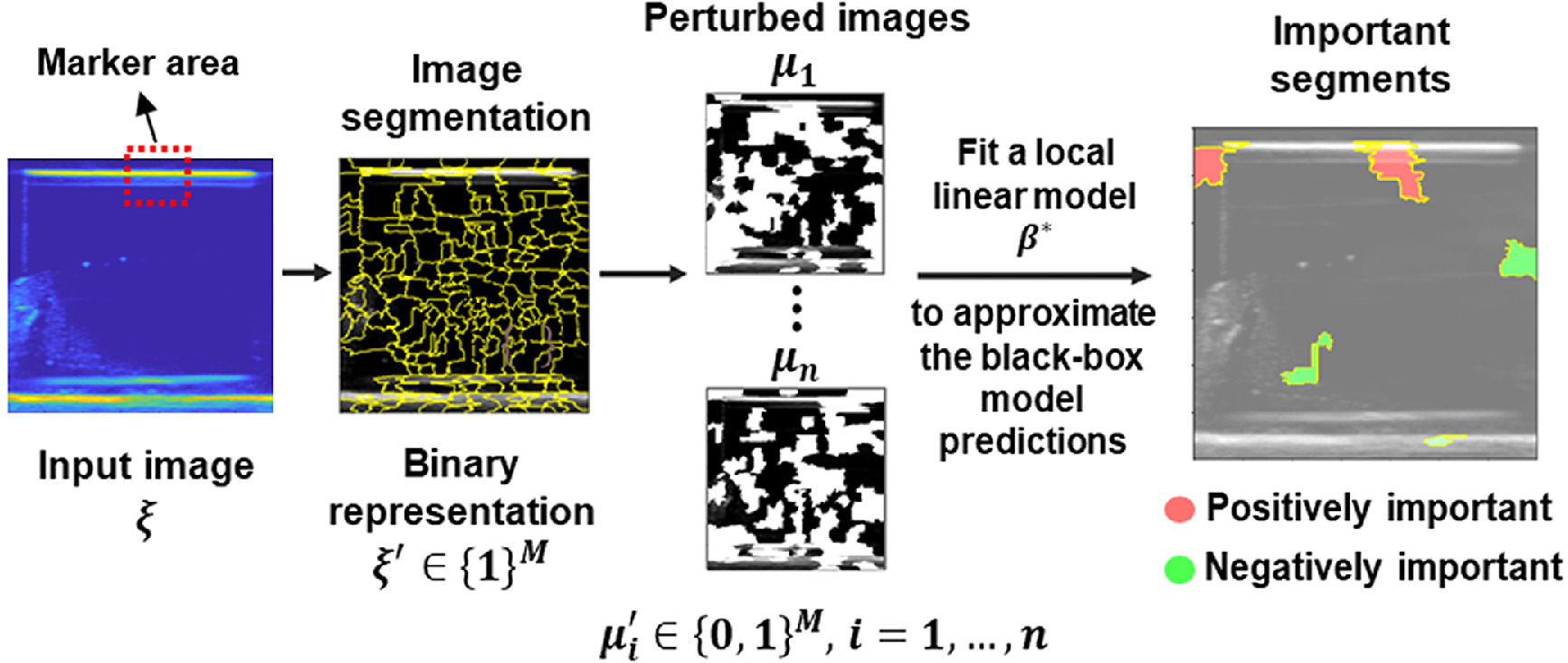
 ;
;
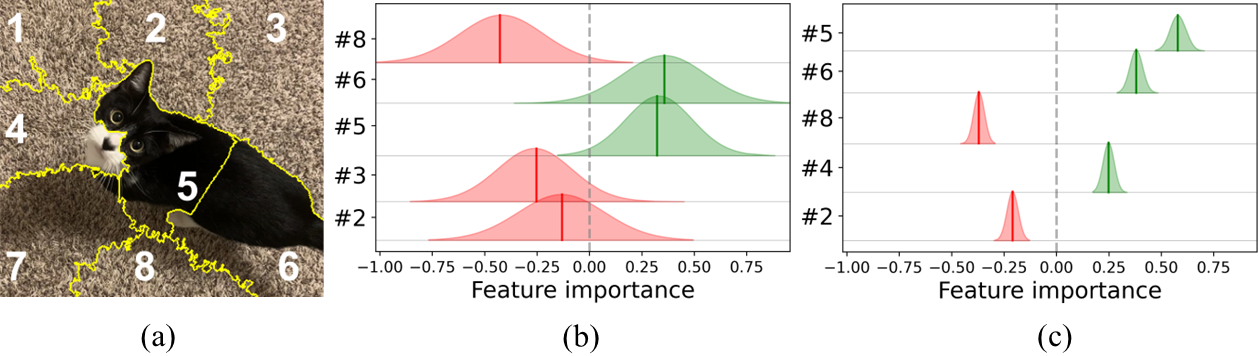
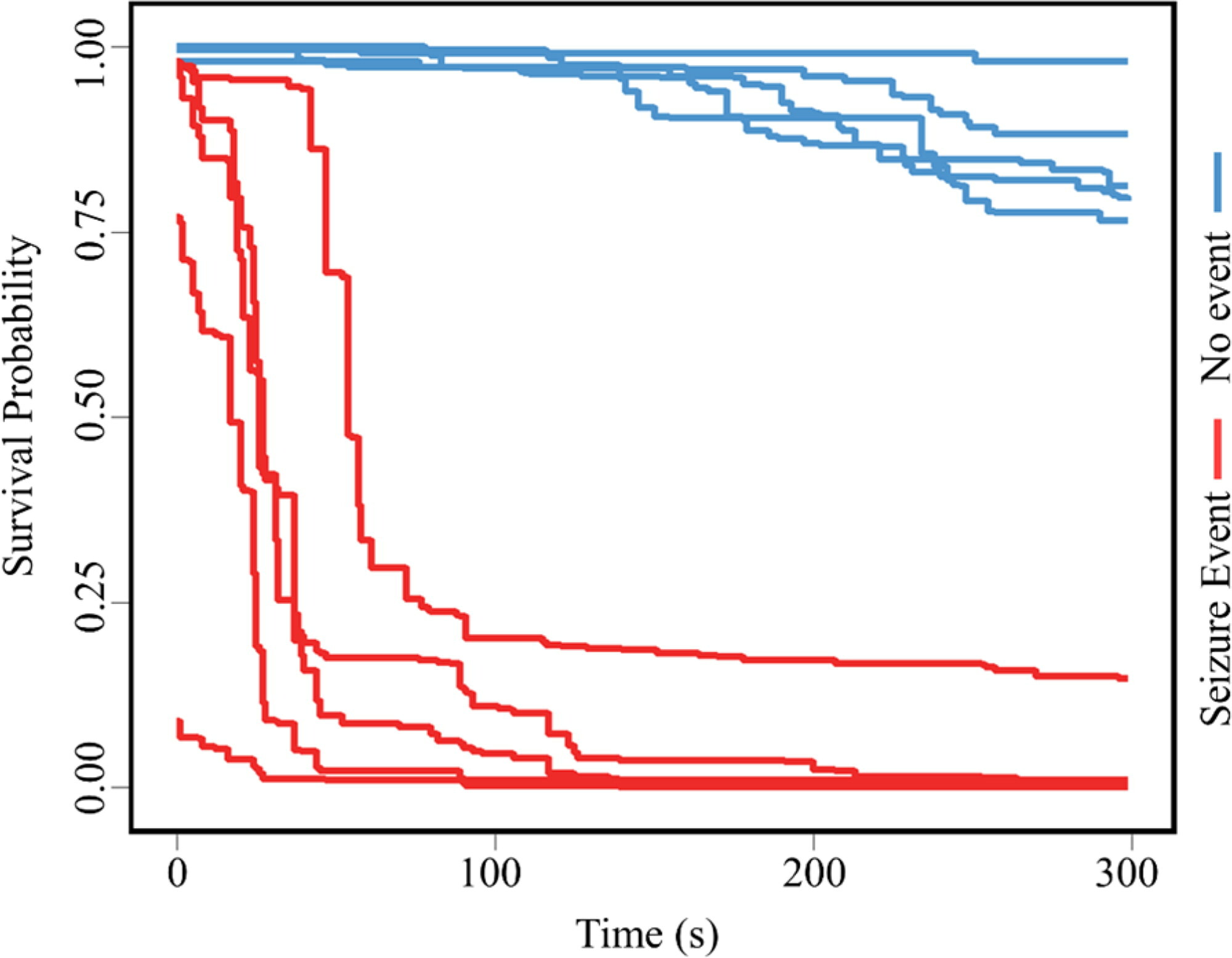
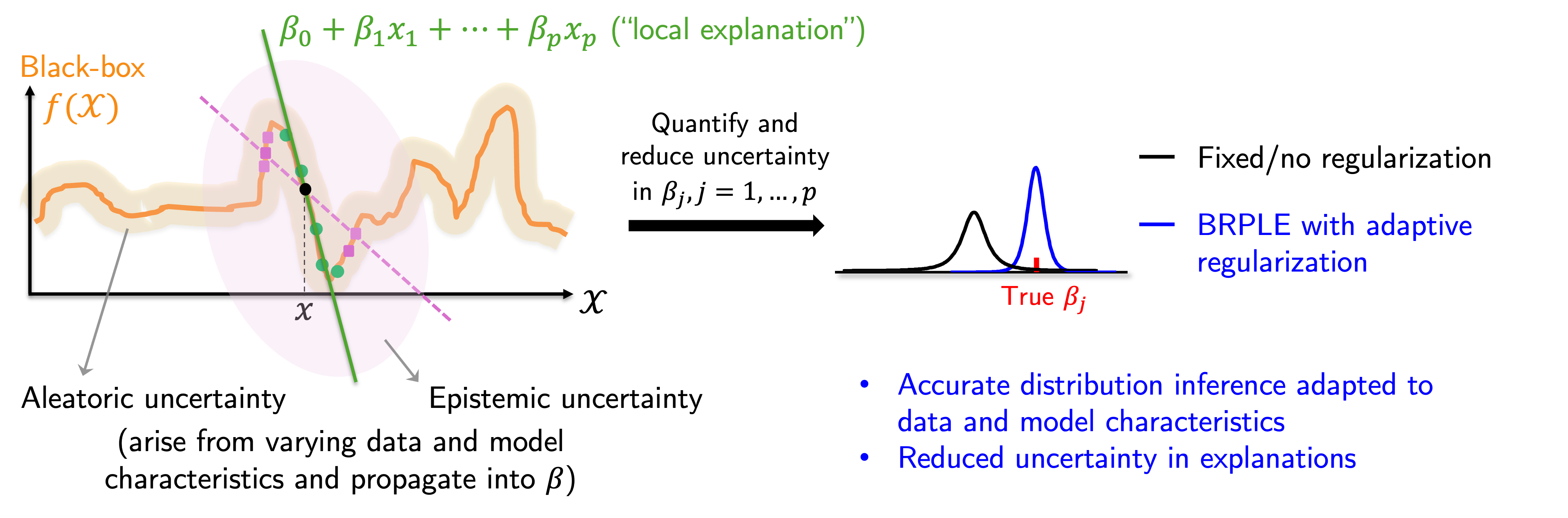
In emerging engineering fields where domain knowledge is unavailable or limited, complex machine learning (ML) models have demonstrated remarkable capabilities in extracting knowledge from data and making accurate predictions. However, their complexity impedes human understanding of their operational mechanisms, which not only diminishes their trustworthiness but also limits broader applications such as knowledge discovery. Existing local post-hoc methods for explaining ML models often produce inconsistent or unreliable results, due to their limited capacity to quantify underlying uncertainty and adapt to diverse data and model characteristics. We propose a Bayesian regularization-based approach to generate local explanations for ML models (i.e., the influence of input features on the output) with enhanced uncertainty quantification and reduction. Our approach leverages linear approximation and posterior inference within a hierarchical Bayesian framework to flexibly adjust regularization based on given data. Through theoretical analysis and extensive case studies, we show that our approach outperforms state-of-the-art methods in capturing and addressing aleatoric (irreducible) and epistemic (reducible) explanation uncertainty, and we highlight the critical role of adaptive regularization in this improvement.